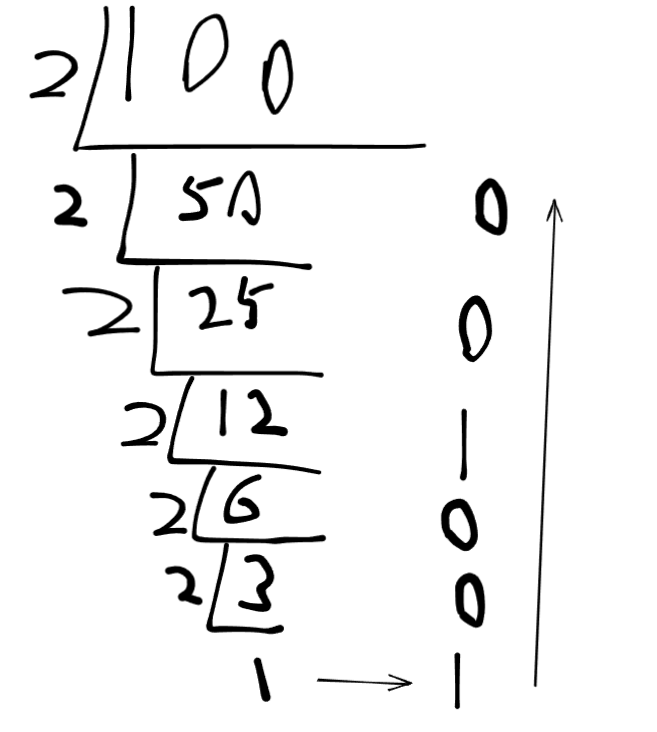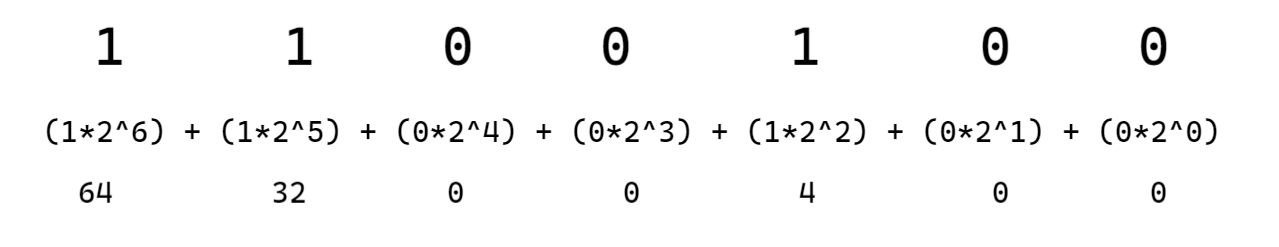3.1 KiB
3.1 KiB
进制转换
了解进制
在了解进制之前，我们先了解一下什么是进制，以及常见的一些进制，首先像我们平常日常生活中用到的就是十进制，十进制就是每逢十就近一位，就比如9+1，9加1后的值是10，我们把10读作十，99+1后的值是100；就是说我们十进制中的每一位到达9之后在加1就会进位；看到刚才的例子想必已经能够明白二进制是怎么回事了，也能够明白二进制为什么没有2了。
进制的缩写和形式表示
| 英文名称 | 简写 | 示例 | |
|---|---|---|---|
| 十进制 | Decimal | D | 1111D 十进制通常会省略掉后面的D |
| 二进制 | Binary | B | 1111B |
| 八进制 | Octal | O | 1111O |
| 十六进制 | Hexadecimal | H | 1111H 十六进制9之后的值分别用A\B\C\D\E\F表示 其中A代表十 F代表十六 |
0-15 在各进制中所展示的值
| 十进制 | 八进制 | 十六进制 | 二进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 01 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 10 | 8 | 1000 |
| 9 | 11 | 9 | 1001 |
| 10 | 12 | A | 1010 |
| 11 | 13 | B | 1011 |
| 12 | 14 | C | 1100 |
| 13 | 15 | D | 1101 |
| 14 | 16 | E | 1110 |
| 15 | 17 | F | 1111 |
十进制二进制互转
十进制转二进制（整数）
转换方法：十进制数除以2，直到商小于2，从的到的最底层商开始向上取余数（包括最后得到的商），得到的余数就是转换后的二进制
示例：100D转换为二进制的过程
将下图计算后的余从低向上进行取值得到的二进制值为1100100B
十进制转二进制（小数）
小数的转换和整数的转换方式有所不同，存在小数的十进制数转换二进制时需要分开处理
小数的处理方式是对小数部分乘2取整，再去小数部分继续乘2取整，直到得到所需的位数或精度位置。
示例 100.0625
二进制转十进制（整数）
位权值相加
示例：1100100B转换为十进制
位权值相加后得出十进制为100
